Записать уравнение динамики вращательного движения. Основное уравнение динамики вращательного движения
Работа при вращении тела идет на увеличение его кинетической энергии . Поскольку , то или .
Учитывая, что , получим . Следовательно, момент силы,
действующей на тело, равен произведению момента инерции тела на угловое ускорение. Если ось вращения совпадает со свободной осью (см. 7.7), то имеет место векторное равенство
Это равенство представляет собой основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Пример 4.5.1. Тонкий стержень длиной и массой вращается вокруг неподвижной оси с угловым ускорением . Ось вращения перпендикулярна стержню и проходит через его середину. Определить момент силы, действующий на стержень.
| |
Согласно основному уравнению динамики вращательного движения вращающий момент связан с угловым ускорением следующим соотношением: ; где момент инерции стержня относительно оси вращения. Т.к. ось вращения проходит через центр масс стержня, то .
Следовательно, момент силы, действующий на стержень, .
Ответ: .
Пример 4.5.2. Вал в виде сплошного цилиндра массой насажен на горизонтальную ось. На цилиндр намотан нерастяжимый шнур, к свободному концу которого подвешена гиря массой . С каким ускорением будет опускаться гиря, если ее предоставить самой себе?
| |
Сделаем чертеж (рис. 4.5.1). Груз опускается с ускорением . На него действуют силы тяжести и натяжения шнура . Вал вращается против часовой стрелки с угловым ускорением . На вал действуют силы тяжести , сила реакции со стороны оси, на которую вал опирается, и сила реакции со стороны шнура . Вращающий момент создает только сила , т.к. линия действия сил и проходит через ось вращения (плечо этих сил равно 0).
Основное уравнение динамики поступательного движения груза имеет вид:
. В проекции на ось Oy: .
Основное уравнение динамики вращательного движения вала имеет вид: .
Если сила, действующая на тело, создает момент, способствующий вращению в заданном направлении, то ее момент считаем положительным (направление вектора момента силы совпадает с направлением углового ускорения ), если препятствует – момент считаем отрицательным (направления и противоположны). Следовательно, в скалярной форме (в проекции на направление углового ускорения) основное уравнение динамики вращательного движения будет иметь вид: .
Учитывая, что ось вращения проходит через центр масс цилиндрического вала перпендикулярно плоскости его основания , где радиус основания цилиндра, а вращающий момент (плечо силы равно радиусу основания цилиндра), то.
По третьему закону Ньютона (шнур нерастяжим), поэтому . Тангенциальное ускорение точек, лежащих на ободе вала, связано с его угловым ускорением соотношением: . С таким же ускорением движется любая точка шнура, на котором подвешен груз. Следовательно, , откуда . Подставив в уравнение (1), получим:и .
Ответ: .
Пример 4.5.3. Через блок в виде диска, имеющего массу , перекинута тонкая гибкая нить, к концам которой подвешены грузы массами и . С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.
Решение:
Сделаем чертеж (рис. 4.5.2). Первый груз будет двигаться поступательно вверх с ускорением , второй – опускаться с таким же ускорением. Уравнения поступательного движения грузов в векторной форме имеют вид .
В проекции на направление оси :
, откуда .
Согласно основному уравнению динамики вращательного движения . При движении грузов диск ускоренно вращается по часовой стрелке, следовательно, сила способствует вращению , а сила тормозит вращение . Поэтому в скалярной форме (в проекции на направление углового ускорения), т.к. плечо сил равно радиусу диска .
Учитывая, что момент инерции диска , а линейное ускорение грузов равно
тангенциальному ускорению точек обода диска, связанного с угловым ускорением соот-
ношением , то , откуда . . В скалярной форме (в проекции на направление углового ускорения)
Ответ: .
Билет1.
Световая волна. Интерференция световых волн.
Свет - в физической оптике электромагнитное излучение, воспринимаемое человеческим глазом. В качестве коротковолновой границы спектрального диапазона, занимаемого светом, принят участок сдлинами волн в вакууме 380-400 нм (750-790 ТГц), а в качестве длинноволновой границы - участок 760-780 нм (385-395 ТГц).В широком смысле, используемом вне физической оптики, светом часто называ
|
Билет2
Билет №3
1. Кинематика вращательного движения. Связь между векторами v и ω.
вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси. Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
Единица измерения угловой скорости радиан в секунду (рад/с).
Таким образом, вектор ω
определяет направление и быстроту вращения. Если ω=const
, то вращение называется равномерным.
Угловая скорость может быть связана с линейной скоростью υ
произвольной точки А
. Пусть за время Δt
точка проходит по дуге окружности длину пути Δs
. Тогда линейная скорость точки будет равна:
/////////////
При равномерном вращении его можно охарактеризовать периодом вращенияТ – временем, за которое точка тела совершает один полный оборот, т.е. поворачивается на угол 2π:
/////////////////
Число полных оборотов, совершаемых телом при равномерном движении по окружности, в единицу времени называется частотой вращения:
….....................
Откуда
Для характеристики неравномерного вращения тела вводится понятие углового ускорения. Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
////////////////////////(1.20)
Выразим тангенциальную и нормальную составляющие ускорения точки A вращающегося тела через угловую скорость и угловое ускорение:
////////////////(1.21)
/////////////////(1.22)
В случае равнопеременного движения точки по окружности (ε=const ):
////////////////////////////
Где ω0
- начальная угловая скорость.Поступательное и вращательное движения твердого тела являются лишь простейшими типами его движения. В общем случае движение твердого тела может быть весьма сложным. Однако в теоретической механике доказывается, что любое сложное движение твердого тела можно представить как совокупность поступательного и вращательного движений.
Кинематические уравнения поступательного и вращательного движений сведены в табл. 1.1.
Таблица 1.1
2. Уравнения Максвелла.06
Первую пару уравнений Максвелла образуют
Первое из этих уравнений связывает значения Е с временными изменениями вектора В и является по существу выражением закона электромагнитной индукции. Второе уравнение отражает то свойство вектора В, что его линии замкнуты (или уходят в бесконечность)
//////////
Билет №4
Билет №5
Работа. Мощность.
Работой называется скалярная величина, равная произведению проекции силы на направление перемещения и пути s ,проходимого точкой приложения силыA fs cos (1.53)Если сила и направление перемещения образуют острый угол (cosα>0), работа положительна. Если угол α – тупой (cosα<0),работа отрицательна. При α = π/2 работаравна нулю
Скалярное произведение двух векторов равно:AB AB cos.Выражение для работы (1.54) можно записать в виде скалярного произведения
Где под Δs подразумевается вектор элементарного перемещения, который мы ранее обозначали через Δr. s vt ////////////
Мощность W есть величина, равная отношению работы ΔА к промежутку времени Δt , за который она совершается:///////////////////////
Если работа меняется со временем, то вводится мгновенное значение мощности:///////////
Билет №6
Уравнения Максвелла.
2. Дифракция Френеля от простейших преград.
Билет №7
Билет№8
Билет №9
В состоянии равновесия
сила mg уравновешива ется упругой силой k Δl0 :
mg k l 0 (1.129)
0 f mg k (l x )
f kx (1.130)
Силы такого вида принято
Называть квазиупругими
Амплитудой колебания.
Величина, стоящая в скобках под знаком
Начальной фазой колебания.
промежуток времени Т, за который фаза
колебания получает приращение, равное 2π
Циклической частотой.
0 2 (1.139)
Энергия гармонического
Колебания
Продифференцировав (1.135) по времени,
Совпадает со средним
значением Ep и равно Е/ 2.
Ток индукционным.
Величина индукционного тока определяется
лишь скоростью изменения Φ, т. е. значением
производной d Φ/d t. При изменении знака
Тока.
Явление электромагнитной
Индукции.
Привило Ленца гласит, что индукционный ток всегда
Его вызывающей.
Билет№10
Нуль
Разделив это выражение на L и заменив через
(2.188);
Заменяя ω0 по формуле (2.188), получим
Свободные затухающие
Колебания.
Уравнение колебаний можно получить, исходя из того,
имеет вид:
где ….
Подставляя значение (2.188) для ω0 и (2.196) для β,
Находим, что
Разделив (2.198) на емкость С , получим напряжение
на конденсаторе:
Билет№12
Сила Лоренца равна
Таким образом, движение
Радиус окружности, по
Которой происходит вращение
Определяется формулой
(2.184) с заменой v на v = v
Шаг спирали l можно найти,
умножив v ║ на определяемый
Формулой (2.185) период
обращения Т :
…............
2. Поляризация при двойном лучепреломлении. Двойно́е лучепреломле́ние - эффект расщепления в анизотропных средах луча света на две составляющие. Впервые обнаружен датским ученымРасмусом Бартолином на кристалле исландского шпата. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча. Первый луч продолжает распространяться прямо, и называется обыкновенным (o - ordinary), второй же отклоняется в сторону, и называется необыкновенным (e - extraordinary). Направление колебания вектора электрического поля необыкновенного луча лежит в плоскости главного сечения (плоскости, проходящей через луч и оптическую ось кристалла). Оптическая ось кристалла - направление в оптически анизотропном кристалле, по которому луч света распространяется, не испытывая двойного лучепреломления.
Нарушение закона преломления света необыкновенным лучом связанно с тем, что скорость распространения света (а значит и показатель преломления) волн с такой поляризацией, как у необыкновенного луча, зависит от направления. Для обыкновенной волны скорость распространения одинакова во всех направлениях.
Можно подобрать условия, при которых обыкновенный и необыкновенный лучи распространяются по одной траектории, но с разными скоростями. Тогда наблюдается эффект изменения поляризации. Например, линейно поляризованный свет, падающий на пластинку можно представить в виде двух составляющих (обыкновенной и необыкновенной волн), двигающихся с разными скоростями. Из-за разности скоростей этих двух составляющих, на выходе из кристалла между ними будет некоторая разность фаз, и в зависимости от этой разности свет на выходе будет иметь разные поляризации. Если толщина пластинки такова, что на выходе из неё один луч на четверть волны (четверть периода) отстаёт от другого, то поляризация превратится в круговую (такая пластинка называется четвертьволновой), если один луч от другого отстанет на пол волны, то свет останется линейно поляризованным, но плоскость поляризации повернётся на некоторый угол, значение которого зависит от угла между плоскостью поляризации падающего луча и плоскостью главного сечения (такая пластинка называется полуволновой).Качественно явление можно объяснить следующим образом. Из уравнений Максвелла для материальной среды следует, что фазовая скорость света в среде обратно пропорциональна величине диэлектрической проницаемостиε среды. В некоторых кристаллах диэлектрическая проницаемость - тензорная величина - зависит от направления электрического вектора, то есть от состояния поляризации волны, поэтому и фазовая скорость волны будет зависеть от ее поляризации. Согласно классической теории света, возникновение эффекта связано с тем, что переменное электромагнитное поле света заставляет колебаться электроны вещества, и эти колебания влияют на распространение света в среде, а в некоторых веществах заставить электроны колебаться проще в некоторых определённых направлениях.Искусственное двойное лучепреломление. Помимо кристаллов двойное лучепреломление наблюдается и визотропных средах, помещённых в электрическое поле (эффект Керра), в магнитное поле (эффект Коттона - Мутона, эффект Фарадея), под действием механических напряжений (фотоупругость). Под действием этих факторов изначально изотропная среда меняет свои свойства и становится анизотропной. В этих случаях оптическая ось среды совпадает с направлением электрического поля, магнитного поля, направлением приложения силы.Отрицательные кристаллы - одноосные кристаллы, в которых скорость распространения обыкновенного луча света меньше, чем скорость распространения необыкновенного луча. В кристаллографии Отрицательными кристаллами называют также жидкие включения в кристаллах, имеющие ту же форму, что и сам кристалл.Положительные кристаллы - одноосные кристаллы, в которых скорость распространения обыкновенного луча света больше, чем скорость распространения необыкновенного луча.
Билет№13
Излучение диполя.06
Называется элементарным
Дипольный электрический
Момент такой системы равен
p ql cost n pm cost , (2.228)
где l – удвоенная амплитуда
Ленный вдоль оси диполя,
pm = ql n
Волновой фронт в так называемой волновой зоне, т. е.
Зависимость
Интенсивности волны от
угла θ изображается с
Помощью диаграммы
Направленности диполя
(рис. 246).
Энергия, излучаемая по всем направлениям в
Излучения.
Билет№14
Данной точке.
Отрицателен
Осью диполя.
Найдем напряжен-
Ность поля на оси
Диполя, а также на
Прямой, проходя-
Щей через центр
Диполя и перпен-
Дикулярной к его
оси (рис. 4).
Положение точек
Будем характеризо-
Вать их расстояни-
ем r от центра дипо-
ля. Напомним, что
r >> l .
На оси диполя векторы Е+ и Е– имеют противополож-
Следует, что
….........
Билет№15
Энергия
Физическая величина, характеризующая
Скоростью и,
во-вторых, нахождением тела в
Потенциальном поле сил.
Энергия первого вида называется
Вектора v.
Умножив на m числитель и знаменатель,
уравнение (1.65) можно переписать как:
Кинетической энергии
…..........
A T 2 T1 (1.67)
Потенциальная энергия
Тел, образующих систему
…...........
Закон сохранения энергии
E E 2 E 1 A н. к. (1.72)
Для системы из N тел, между которыми
Линия напряженности.
Поток вектора напряженности
Густота линий выбирается так, чтобы количество
Вектора Е.
Линии Е точечного заряда представляют собой
радиальные прямые.
Следовательно, полное число линий N равно
Если площадка dS ориентирована так, что нормаль к
ней образует с вектором Е угол α, то количество
Нормали к площадке
численно равно
…..........
где выражение для Ф называется потоком вектора Е
В тех местах, где вектор Е
Объем, охватываемых поверх-
ностью), Еn и соответственно d Ф
будут отрицательны (рис. 10)
Теорема Гаусса
Можно показать, что, как и для сферической
Билет№16
Изменения.
Инерциальные системы
Отсчета
Система отсчета, в которой выполняется
Неинерциальной.
Примером инерциальной системы
Инерциальной
Групповая скорость - это величина, характеризующая скорость распространения «группы волн» - то есть более или менее хорошо локализованной квазимонохроматической волны (волны с достаточно узким спектром). Групповая скорость во многих важных случаях определяет скорость переноса энергии и информации квазисинусоидальной волной (хотя это утверждение в общем случае требует серьёзных уточнений и оговорок).
Групповая скорость определяется динамикой физической системы, в которой распространяется волна (конкретной среды, конкретного поля итп). В большинстве случаев подразумевается линейность этой системы (точно или приближенно).
Для одномерных волн групповая скорость вычисляется из закона дисперсии:
,
где - угловая частота, - волновое число.
Групповая скорость волн в пространстве (например, трехмерном или двумерном) определяется градиентомчастоты по волновому вектору :
Замечание: групповая скорость вообще говоря зависит от волнового вектора (в одномерном случае - от волнового числа), то есть вообще говоря различна для разной величины и для разных направлений волнового вектора.
Билет№17
Работа сил
Электростатического поля
….......
…........
…........
мы учли, что
….....
Отсюда для работы на пути 1–2 получаем
Следовательно, силы, действующие на заряд q" в
поле неподвижного заряда q , являются
потенциальными.
где El – проекция вектора Е на направление
элементарного перемещения d l
Циркуляцией по контуру.
Таким образом, для электростатического
Потенциал.
Для разных пробных значений q′ отношение
Wp/qпр будет постоянным
ведичина φ ─ называется потенциалом поля
Электрических полей
Из 225 и226 получаем
С учетом (2.23) получаем
….......
Для потенциальной энергии заряда q′ в поле
Отдельности
Из 226 вытекает что
Средах
Однородном веществе
Примеры мутных сред:
– дым (мельчайшие твердые частицы в газе)
– туман (капли жидкости в воздухе, газе)
– суспензия клеток
– эмульсия (дисперсная система, состоящая из
Другие виды энергии
Поглощающего вещества
….......
…........
….....
Билет№18
Второй закон Ньютона.02
Тела.
Связь между напряженностью
Направление r равна
Можно написать
Щении вдоль касательной к
поверхности τ на величину d τ
Потенциал не изменится, так
что φ/τ = 0. Но φ/τ равна
Циальной поверхности будет
Совпадать с направлением
Же точке.
Билет№19
Конденсаторы
Под емкостью конденсатора понимается физическая
величина, пропорциональная заряду q и обратно
Соединение конденсаторов
При параллельном соединении (рис. 50) на каждой из
Напряжение
Обкладках.
Поэтому напряжение на каждом из
конденсаторов:
Закон Кирхгофа.
Билет№20
Можно придать другой вид
…..............
Векторную величину
p m v (1.44)
Закон сохранения импульса
Импульсом системы р называется
Образующих систему,
…....................
Центром тяжести системы.
Скорость центра инерции получается
путем дифференцирования rс по
времени:
.................
Учитывая, что mi vi есть рi , а Σрi дает
импульс системы р, можно написать
p m v c(1.50)
Таким образом, импульс системы равен
Каждой из внутренних сил
По третьему закону
Ньютона можно написать fij
= – fji
Символом Fi обозначена
Результирующая внешних
сил, действующая на тело i
Уравнение (1.45)
…......
….........
…..........
Нулю, вследствие чего
Р постоянен
Постоянным
p m vc (1.50)
Энергия системы зарядов.02
Рассмотрим систему из двух точечных зарядов q 1 и q 2,
находящихся на расстоянии r 12.
Работа переноса заряда q 1 из бесконечности в точку,
удаленную от q 2 на r 12 равна:
где φ 1 – потенциал, создаваемый зарядом q 2 в той
точке, в которую перемещается заряд q 1
Аналогично для второго заряда получим:
…........
Равна энергии трех зарядов
…...............
….....................
где φ1 – потенциал, создаваемый зарядами q 2 и q 3 в той
точке, где расположен заряд q 1 и т. д.
Добавляя к системе зарядов последовательно
q4, q 5 и т. д., можно убедиться в том, что в
случае N зарядов потенциальная энергия
Системы равна
где φi – потенциал, создаваемый в той точке,
где находится qi , всеми зарядами, кроме i -го.
Билет№21
Сила
Выражение (2.147) совпадает с (2.104), если положить
k = 1. Следовательно, в СИ закон Ампера имеет вид
df i d lB (2.148)
df iB dl sin (2.149)
Сила Лоренца
Согласно (2.148) на элемент тока d l действует в
магнитном поле сила
df i d lB (2.150)
Заменив id l через S jdl [см. (2.111)], выражению закона
Ампера можно придать вид
df Sdl jB jBdV
где dV – объем проводника, к которому приложена
сила d f.
Разделив d f на dV , получим «плотность силы», т. е.
силу, действующую на единицу объема проводника:
f ед. об jB (2.151)
Найдем, что
fед. об ne "uB
Эта сила равна сумме сил, приложенных к носителям
в единице объема. Таких носителей n , следователь-
Важно отметить, что закон говорит только об общей излучаемой энергии. Распределение энергии по спектруизлучения описывается формулой Планка, в соответствии с которой в спектре имеется единственный максимум, положение которого определяется законом Вина.
Зако́н смеще́ния Ви́на даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела. λmax = b /T ≈ 0,002898 м·К × T −1 (K),
где T - температура, а λmax - длина волны с максимальной интенсивностью. Коэффициент b , называемыйпостоянной Вина, в системе СИ имеет значение 0,002898 м·К.
Для частоты света (в герцах) закон смещения Вина имеет вид:
α ≈ 2,821439… - постоянная величина (корень уравнения
),
k - постоянная Больцмана,
h - постоянная Планка,
T - температура (в кельвинах).
Билет№22
Третий закон Ньютона.
Направлению.
f12 f21 (1.42)
Билет№23
Формула Планка.
Билет№24
Билет№25
Закон Джоуля – Ленца.
Фотоэффект.
Билет№26
Эффект Комптона.
Билет1.
Основное уравнение динамики вращательного движения.
Это основное уравнение динамики вращательного движения тела: угловое ускорение вращающегося тела прямо пропорционально сумме моментов всех действующих на него сил относительно оси вращения тела и обратно пропорционально моменту инерции тела относительно этой оси вращения. Полученное уравнение аналогично по форме записи выражению второго закона Ньютона для поступательного движения тела.
второй закон Ньютона для вращательного движения По определению угловое ускорение и тогда это уравнение можнопереписать следующим образом с учетом (5.9) или
Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела , равно импульсу момента всех внешних сил, действующих на это тело.
Динамика вращательного движения твердого тела. Основное уравнение динамики вращательного движения. Момент инерции твердого тела относительно оси. Теорема Штейнера. Момент импульса. Момент силы. Закон сохранения и изменения момента импульса.
На прошлом занятии разобрали импульс и энергию. Рассмотрим величину момент импульса - характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью проходит вращение. Рассмотрим частицу А. r – радиусвектор, характеризующий положение относительно некоторой точки O, выбранной системы отсчёта. P-импульс в этой системе. Векторная величина L – момент импульса частицы А относительно точки О: Модуль вектора L: где α – угол между r и p, l=r sin α плечо вектора p относительно точки О.
Рассмотрим изменение вектора L со временем: = т. к. dr/dt =v, v направлен так же, как и p , т. к. dp/dt=F –равнодействующая всех сил. Тогда: Момент силы: М= Модуль момента силы: где l – плечо вектора F относительно точки O Уравнение моментов: производная по времени от момента импульса L частицы относительно некоторой точки О равна моменту M равнодействующей силы F относительно той же точки О: Если M = 0, то L=const – если момент равнодействующей силы равен 0 в течении интересующего промежутка времени, то импульс частицы остаётся постоянным в течении этого времени.
Уравнение моментов позволяет: Найти момент силы M относительно точки O в любой момент времени t , если известна зависимость от времени момента импульса L(t) частицы, относительно той же точки; Определить припращение момента импульса частицы относительно точки O за любой промежуток времени, если известна зависимость от времени момента сил M(t), действующего на эту частицу (относительно той же точки О). Используем уравнение моментов, и запишем элементарное приращение вектора L: Тогда, проинтегрировав выражение, найдём приращение L за конечный промежуток времени t: правая часть – импульс момента силы. Приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за это же время.
Момент импульса и момент силы относительно оси Возьмём ось z. Выберем точку О. L - момент импульса частицы А относительно точки, M- момент силы. Моментом импульса и моментом силы относительно оси z называют проекцию на эту ось векторов L и M. Обозначают Lz и Mz - они не зависят от точки выбора О. Производная по времени от момента импульса частицы относительно оси z равна моменту силы относительно этой оси. В частности: Mz=0 Lz=0. Если момент силы относительно некоторой подвижной оси z равен нулю, то момент импульса частицы относительно этой оси остаётся постоянным, при этом сам вектор L может меняться.
Закон сохранения моменте импульса Выберем произвольную систему частиц. Момент импульса данной системы будет векторная сумма моментов импульсов её отдельных частиц: Векторы определены относительно одной и той же оси. Момент импульса величина аддитивная: момент импульса системы равен сумме моментов импульсов её отдельных частей независимо от того, взаимодействуют они между собой или нет. Найдём изменение момента импульса: - суммарный момент всех внутренних сил относительно точки О. ; - суммарный момент всех внешних сил относительно точки О. Производная момента импульса системы по времени равна суммарному моменту всех внешних сил! (используя 3 закон Ньютона):
Момент импульса системы может изменяться под действием только суммарного момента всех внешних сил Закон сохранения импульса: момент импульса замкнутой системы частиц остаётся постоянным, т. е. не меняется со временем. : Справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчёта. Внутри системы изменения могут быть, но приращение момента импульса одной части системы равно убыли момента импульса другой её части. Закон сохранения момента импульса – не является следствием 3 -го закона Ньютона, а представляет самостоятельный общий принцип; один из фундаментальных законов природы. Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
Динамика твёрдого тела Два основных вида движения твёрдого тела: Поступательное: все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения. Задать движение одной точки Вращательное: все точки твёрдого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Задать ось вращения и угловую скорость в каждый момент времени Любое движение твёрдого тела может быть представлена как сумма двух этих движений!
Произвольное перемещение твёрдого тела из положения 1 в положение 2 можно представить как сумму двух перемещенийпоступательного перемещения из положения 1 в положения 1’ или 1’’ и поворота вокруг оси О’ или оси О’’. Элементарное перемещение ds: - «поступательного» - «вращательного» Скорость точки: - одинаковая для всех точек тела скорость поступательного движения - различная для разных точек тела скорость, связанная с вращением тела
Пусть система отсчёта неподвижна. Тогда движение можно рассмотреть как вращательное движение с угловой скоростью w в системе отсчёта, движущейся относительно неподвижной системы поступательно со скоростью v 0. Линейная скорость v’, обусловленная вращением твёрдого тела: Скорость точки при сложном движении: Существуют точки, которые при векторном перемножении векторов r и w дают вектор v 0. Эти точки лежат на одной прямой и образуют мгновенную ось вращения.
Движение твёрдого тела в общем случае определяется двумя векторными уравнениями: Уравнение движения центра масс: Уравнение моментов: Законы действующих внешних сил, точки их приложения и начальные условия скорость и положение каждой точки твердого тела в любой момент времени. Точки приложения внешних сил можно переносить вдоль направления действия сил. Равнодействующая сила- сила, сила которая равна результирующей сил F, действующих на твёрдое тело, и создаёт момент, равный суммарному моменту M всех внешних сил. Случай поля тяжести: равнодействующая сил тяжести проходит через центр масс. Сила, действующая на частицу: Суммарный момент сил тяжести относительно любой точки:
Условия равновесия твердого тела: тело будет оставаться в состоянии покоя, если нет причин, вызывающих его движение. По двум основным уравнениям движения тела, для это необходимо два условия: Результирующая внешних сил равна нулю: Сумма моментов всех внешних сил, действующих на тело относительно любой точки должен быть равен нулю: Если система неинерциальная, то кроме внешних сил необходимо учитывать силы инерции (силы, обусловленные ускоренным движением неинерциальной системы отсчета относительно инерциальной системы отсчета). Три случая движения твёрдого тела: Вращение вокруг неподвижной оси Плоское движение Вращение вокруг свободных осей
Вращение вокруг неподвижной оси Момент импульса твёрдого тела относительно оси вращения ОО’: где mi и pi- масса и расстояние от оси вращения i-й частицы твёрдого тела, wz –его угловая скорость. Введём обозначение: где I – момент инерции твёрдого тела относительно оси OO’: Момент инерции тела находится как: где dm и dv – масса и объём элемента тела, находящегося на расстоянии r от интересующей нас оси z; ρ- плотность тела в данной точке.
Моменты инерции однородных твёрдых тел, относительно оси проходящей через центр масс: Теорема Штейнера: момент инерции I относительно произвольной оси z равен моменту инерции Ic относительно оси Ic, параллельной данной и проходящей через центр масс C тела, плюс произведение массы m тела на квадрат расстояния a между осями:
Уравнение динамики вращения твёрдого тела: где Mz – суммарный момент всех внешних сил относительно оси вращения. Момент инерции I определяет инерционные свойства твёрдого тела при вращении: при одном и том же значении момента сил Mz тело с большим моментом инерции приобретает меньшее угловое ускорения βz. Mz включает и моменты сил инерции. Кинетическая энергия вращающегося твёрдого тела (ось вращения неподвижна): пусть скорость частицы вращающегося твёрдого тела – Тогда: где I – момент инерции относительно оси вращения, w – его угловая скорость. Работа внешних сил при вращении твердого тела вокруг неподвижной оси определяется действием момента Mz этих сил относительно данной оси.
Плоское движение твёрдого тела При плоском движении центра масс твердого тела движется в определённой плоскости, неподвижной в данной системе отсчёта К, а вектор его угловой скорости w перпендикулярен этой плоскости. Движение описывают два уравнения: где m – масса тела, F-результирующая всех внешних сил, Ic и Mcz- момент инерции и суммарный момент всех внешних сил- оба относительно оси, проходящей через центр тела. Кинетическая энергия твёрдого тела при плоском движении складывается из энергии вращения в системе вокруг оси, проходящей центр масс, энергии связанной с движением центра масс: где Ic –момент инерции относительно оси вращения (через ЦМ), w – угловая скорость тела, m – его масса, Vc – скорость центра масс тела системе отсчёта K.
Вращение вокруг свободных осей Ось вращения, направление которой в пространстве остаётся неизменным без действия на неё каких либо сил извне, называют свободной осью вращения тела. Главные оси тела – три взаимно перпендикулярные оси, проходящие через его центр масс, которые могут служить свободными осями. Для удержания оси вращения в неизменном направлении к ней необходимо приложить момент M некоторых внешних сил F: Если угол равен 90 градусам, то L совпадает по направлению с w, т. е. М=0!- направление оси вращения будет оставаться неизменным без внешнего воздействия При вращении тела вокруг любой главной оси вектор момента импульса L совпадает по направлению с угловой скоростью w: где I -момент инерции тела относительно данной оси.
Уравнения динамики твердого тела. Общий случай.
В общем случае абсолютно твердое тело имеет 6 степеней свободы, и для описания его движения необходимы 6 независимых скалярных уравнений или 2 независимых векторных уравнения.
Вспомним, что твердое тело можно рассматривать как систему материальных точек, и, следовательно, к нему применимы те уравнения динамики, которые справедливы для системы точек в целом.
Обратимся к опытам.
Возьмем резиновую палку, утяжеленную на одном из концов и имеющую лампочку точно в центре масс (рис. 3.1). Зажжем лампочку и бросим палку из одного конца аудитории в другой, сообщив ей произвольное вращение - траекторией лампочки будет при этом парабола - кривая, по которой полетело бы небольшое тело, брошенное под углом к горизонту.
Стержень, опирающийся одним из концов на гладкую горизонтальную плоскость (рис. 1.16), падает таким образом, что его центр масс остается на одной и той же вертикали - нет сил, которые сдвинули бы центр масс стержня в горизонтальном направлении.
Опыт, который был представлен на рис. 2.2а,в, свидетельствует о том, что для изменения момента импульса тела существенна не просто сила, а ее момент относительно оси вращения.
Тело, подвешенное в точке, не совпадающей с его центром масс (физический маятник), начинает колебаться (рис. 3.2а) - есть момент силы тяжести относительно точки подвеса, возвращающий отклоненный маятник в положение равновесия. Но тот же маятник, подвешенный в центре масс, находится в положении безразличного равновесия (рис. 3.26).
Роль момента силы наглядно проявляется в опытах с “послушной” и “непослушной” катушками (рис. 3.3). Плоское движение этих катушек можно представить как чистое вращение вокруг мгновенной оси, проходящей через точку соприкосновения катушки с плоскостью. В зависимости от направления момента силы относительно мгновенной оси катушка либо откатывается (рис. 3.3а), либо накатывается на нитку (рис. 3.36). Держа нить достаточно близко к горизонтальной плоскости, можно принудить к послушанию самую “непослушную” катушку.
Все эти опыты вполне согласуются с известными законами динамики, сформулированными для системы материальных точек: законом движения центра масс и законом изменения момента импульса системы под действием момента внешних сил. Таким образом, в качестве двух векторных уравнений движения твердого тела можно использовать:
1. Уравнение движения центра масс
Здесь - скорость центра масс тела, сумма всех внешних сил, приложенных к телу.
2. Уравнение моментов
Здесь - момент импульса твердого тела относительно некоторой точки, М - суммарный момент внешних сил относительно той же самой точки.
К уравнениям (3.1) и (3.2), являющимся уравнениями динамики твердого тела, необходимо дать следующие комментарии:
1. Внутренние силы, как и в случае произвольной системы материальных точек, невлияют на движение центра масс и не могут изменить момент импульса тела.
2. Точку приложения внешней силы можно произвольно перемещать вдоль линии, по которой действует сила. Это следует из того, что в модели абсолютно твердого тела локальные деформации, возникающие в области приложения силы, в расчет не принимаются. Указанный перенос не повлияет и на момент силы относительно какой бы то ни было точки, так как плечо силы при этом не изменится.
3. Векторы и М в уравнении (3.2), как правило, рассматриваются относительно некоторой неподвижной в лабораторной системе точки. Во многих задачах и М удобно рассматривать относительно движущегося центра масс тела. В этом случае уравнение моментов имеет вид, формально
совпадающий с (3.2). В самом деле, момент импульса тела относительно движущегося центра масс О связан с моментом импульса относительно неподвижной точки О соотношением, полученным в конце лекции №2:
где - радиус-вектор от О к - полный импульс тела. Аналогичное соотношение легко может быть получено и для моментов силы:
где - геометрическая сумма всех сил, действующих на твердое тело. Поскольку точка О неподвижна, то справедливо уравнение моментов (3.2):
Здесь учтено, что
Величина есть скорость точки О в лабораторной системе Учитывая (3.4), получим
Поскольку движущаяся точка О - это центр масс тела, то масса тела), то есть уравнение моментов относительно движущегося центра масс имеет такой же вид, что и относительно неподвижной точки. Существенно отметить, что в этом случае, как было показано в конце лекции №2, скорости всех точек тела при определении следует брать относительно центра масс тела.
Ранее было показано, что произвольное движение твердого тела можно разложить на поступательное (вместе с системой начало которой находится в некоторой точке - полюсе, жестко связанном с телом) и вращательное (вокруг мгновенной оси, проходящей через полюс). С точки зрения кинематики выбор полюса особого значения не имеет, с точки же зрения динамики полюс, как теперь понятно, удобно поместить в центр масс. Именно в этом случае уравнение моментов (3.2) может быть записано относительно центра масс (или оси, проходящей через центр масс) в том же виде, как и относительно неподвижного начала (или неподвижной оси).
4. Если не зависит от угловой скорости тела, от скорости центра масс, то уравнения (3.1) и (3.2) можно рассматривать
независимо друг от друга. В этом случае уравнение (3.1) соответствует просто задаче из механики точки, а уравнение (3.2) - задаче о вращении твердого тела вокруг неподвижной точки или неподвижной оси. Пример ситуации, когда уравнения (3.1) и (3.2) нельзя рассматривать независимо - движение вращающегося твердого тела в вязкой среде.
Далее в этой лекции мы рассмотрим уравнения динамики для трех частных случаев движения твердого тела: вращения вокруг неподвижной оси, плоского движения и, наконец, движения твердого тела, имеющего ось симметрии и закрепленного в центре масс.
I. Вращение твердого тела вокруг неподвижной оси.
В этом случае движение твердого тела определяется уравнением
Здесь - это момент импульса относительно оси вращения, то есть проекция на ось момента импульса, определенного относительно некоторой точки, принадлежащей оси (см. лекцию №2). М - это момент внешних сил относительно оси вращения, то есть проекция на ось результирующего момента внешних сил, определенного относительно некоторой точки, принадлежащей оси, причем выбор этой точки на оси, как и в случае с значения не имеет. Действительно (рис. 3.4), где - составляющая силы, приложенной к твердому телу, перпендикулярная оси вращения, - плечо силы относительно оси.
При наблюдении сложных движений, например движения тела человека (ходьба, бег, прыжки и т.д.), кажется трудным или даже невозможным описать перемещение всех его точек. Однако, анализируя такие движения, можно заметить, что они состоят из более простых - поступательных и вращательных перемещений.
Механика поступательного движения известна читателю, поэтому раздел начинается с рассмотрения вращательного движения. Наиболее простым является вращение твердого тела вокруг неподвижной оси. Этот случай позволяет ознакомиться со спецификой, терминологией и законами вращательного движения.
5.1. КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ АБСОЛЮТНО ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Абсолютно твердым телом называют такое, расстояние между любыми двумя точками которого неизменно.
Размеры и форма абсолютно твердого тела не изменяются при его движении.
Понятие «абсолютно твердое тело» - физическая абстракция, так как любое тело способно к деформациям. Однако во многих случаях деформацией можно пренебречь.
Наиболее простой случай вращательного движения абсолютно твердого тела - вращение относительно неподвижной оси. Это такое движение, при котором точки тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения.
Известно, что в некоторых случаях для характеристики движения тела необязательно указывать движение всех его точек; так, например, при поступательном движении достаточно указать движение любой одной точки тела.
При вращательном движении вокруг оси точки тела перемещаются по разным траекториям, но за одно и то же время все точки и само тело поворачивается на одинаковый угол. Для характеристики вращения
проведем в плоскости, перпендикулярной оси, радиус-вектор к некоторой точке i (рис. 5.1). Временная зависимость угла α поворота радиуса-вектора относительно некоторого выделенного направления ОХ является уравнением вращательного движения твердого тела вокруг неподвижной оси:
Быстрота вращения тела характеризуется угловой скоростью, равной первой производной от угла поворота радиуса-вектора по времени:
Угловая скорость есть вектор, который направлен по оси вращения и связан с направлением вращения правилом правого винта (рис. 5.2). Вектор угловой скорости в отличие от векторов скорости и силы является скользящим: у него нет определенной точки приложения, и он может быть расположен в любом месте на оси вращения. Таким образом, задание вектора ω указывает положение оси вращения, направление вращения и модуль угловой скорости.
Быстрота изменения угловой скорости характеризуется угловым ускорением, равным первой производной от угловой скорости по времени:
или в векторной форме:
Из (5.4) видно, что вектор углового ускорения совпадает по направлению с элементарным, достаточно малым изменением вектора угловой скорости dω : при ускоренном вращении угловое ускорение направлено так же, как и угловая скорость, при замедленном вращении - противоположно ей.
Так как угловое перемещение всех точек абсолютно твердого тела одинаково, то, согласно (5.2) и (5.3), одновременно все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение. Линейные характеристики - перемещение, скорость, ускорение - различны для разных точек. Укажем в скалярном виде связь, которая может быть выведена самостоятельно, между линейными и угловыми характеристиками для i-й точки, движущейся по окружности радиусом r i:
Рис. 5.3
В заключение приведем полученные путем интегрирования соответствующих выражений формулы кинематики вращательного движения твердого тела вокруг неподвижной оси:
уравнение равномерного вращательного движения [см. (5.2)]:
зависимость угловой скорости от времени в равнопеременном вращательном движении [см. (5.3)]:
уравнение равнопеременного вращательного движения [см. (5.1) и (5.6)]:
Полезно сопоставить эти формулы с аналогичными зависимостями для поступательного движения.
5.2. ОСНОВНЫЕ ПОНЯТИЯ. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Момент силы _
Пусть к некоторой точке i твердого тела приложена сила F^, лежащая в плоскости, перпендикулярной оси вращения (рис. 5.4).
Моментом силы относительно оси вращения называют векторное произведение радиуса-вектора точки i на силу:
Раскрывая его, можно записать:
где β - угол между векторами r i и F i . Так как плечо силы h i = r i sinβ (см. рис. 5.4), то
Если сила действует под некоторым углом α к плоскости вращения (рис. 5.5), то ее можно разложить на две составляющие. Одна из них лежит в плоскости, перпендикулярной оси вращения, а другая параллельна этой этой оси и не оказывает влияния на вращение тела (в реальном случае она действует лишь на подшипники). Далее будут рассматриваться только силы, лежащие в плоскости, перпендикулярной оси вращения.
Рис. 5.4
Рис. 5.5
Работа во вращательном движении
Пусть при действии силы F i (см. рис. 5.4) тело поворачивается на достаточно малый угол dα. Найдем работу этой силы.
Известное из средней школы выражение для работы силы в данном случае следует записать так:
Итак,
элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела.
Если на тело действует несколько сил, то элементарная работа, совершенная всеми ими, определяется аналогично (5.12):
где М - суммарный момент всех внешних сил, действующих на тело.
Если при повороте тела положение радиуса-вектора изменилось от α 1 до α 2 , то работа внешних сил может быть найдена интегрированием выражения (5.13):
Момент инерции
Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от распределения ее в пространстве относительно оси. Мера инертности тела при вращении характеризуется моментом инерции тела относительно оси вращения. Укажем сначала, что
моментом инерции материальной точки относительно оси вращения называют величину, равную произведению массы точки на квадрат расстояния ее от оси:
Моментом инерции тела относительно оси называют сумму моментов инерции всех материальных точек, из которых состоит тело:
В качестве примера выведем формулу момента инерции тонкого однородного стержня длиной l и массой т относительно оси, перпендикулярной стержню и проходящей через его середину (рис. 5.6). Выберем достаточно малый участок стержня длиной dx и массой dm, удаленный от оси 00" на расстояние х. Ввиду малости этого участка он может быть принят за материальную точку, его момент инерции [см. (5.15)] равен:
Масса элементарного участка равна произведению линейной плотности т/l, умноженной на длину элементарного участка: dm = (m/l) dx Подставив это выражение в (5.18), получим
Чтобы найти момент инерции всего стержня, проинтегрируем выражение (5.19) по всему стержню, т.е. в пределах от -1/2 до +1/2:
Приведем выражения для моментов инерции разных симметричных тел массой т:
полого однородного цилиндра (обруча) с внутренним радиусом r и внешним R относительно оси ОО", совпадающей с геометрической осью цилиндра (рис. 5.7):
сплошного однородного цилиндра (r = 0) или диска [см. (5.21)]:
однородного шара относительно оси, проходящей через его центр:
прямоугольною параллелепипеда относительно оси ОО", проходящей через его центр перпендикулярно плоскости основания (рис. 5.8):
Во всех перечисленных примерах ось вращения проходит через центр масс тела. При решении задач для определения момента инерции тела относительно оси, не проходящей через центр масс, можно воспользоваться теоремой Гюйгенса. Согласно этой теореме, момент инерции тела относительно некоторой оси OO":
где J 0 - момент инерции относительно параллельной оси, проходящей через центр масс тела OO"; т - масса тела; d - расстояние между двумя параллельными осями (рис. 5.9). Единицей момента инерции является килограмм-метр в квадрате (кг-м 2).
Момент импульса
Моментом импульса (момент количества движения) материальной точки, вращающейся относительно некоторой оси, называется величина, равная произведению импульса точки на расстоянии ее до оси вращения:
Момент импульса тела, вращающегося относительно некоторой оси, равен сумме моментов импульсов точек, из которых состоит данное тело:
Так как угловая скорость всех точек твердого тела одинакова, выне-ся ω за знак суммы [см. (5.29)], получим:
(/ - момент инерции тела относительно оси), или в векторной форме:
Итак, момент импульса равен произведению момента инерции точки на угловую скорость. Отсюда следует, что направления векторов момента импульса и угловой скорости совпадают. Единицей момента импульса является килограмм-метр в квадрате в секунду (кг? м 2 ? с -1).
Формулу (5.31) полезно сравнить с аналогичной формулой для импульса в поступательном движении.
Кинетическая энергия вращающегося тела
При вращении тела его кинетическая энергия складывается из кинетических энергий отдельных точек тела. Для твердого тела:
Полезно сопоставить выражение (5.32) с аналогичным выражением для поступательного движения.
Продифференцировав (5.32), получим элементарное изменение кинетической энергии во вращательном движении:
Основное уравнение динамики вращательного движения
Пусть твердое тело, на которое действовали внешние силы, повернулось на достаточно малый угол da. Приравняем элементарную работу всех внешних сил при таком повороте [см. (5.13)] элементарному изменению кинетической энергии [см. (5.33)]: M dα = J ω dω , откуда:
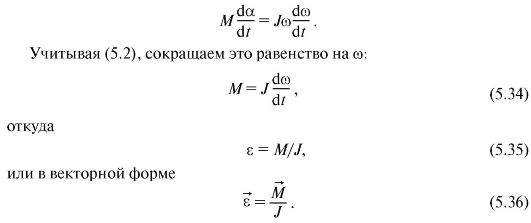
Это и есть основное уравнение динамики вращательного движения. Из (5.35) видно, что момент инерции характеризует инерционные свойства тела во вращательном движении: при действии внешних сил угловое ускорение тела тем больше, чем меньше момент инерции тела.
Основное уравнение для вращательного движения играет ту же роль, что и второй закон Ньютона для поступательного. Физические величины, входящие в это уравнение, аналогичны соответственно силе, массе и ускорению.
Из (5.34) следует, что:
Производная от момента импульса тела по времени равна равнодействующему моменту всех внешних сил.
Зависимость углового ускорения от момента силы и момента инерции можно продемонстрировать с по-
мощью прибора, изображенного на рис. 5.10. Под действием груза 1, подвешенного на нити, перекинутой через блок, крестовина ускоренно вращается. Перемещая грузики 2 на разные расстояния от оси вращения, можно изменять момент инерции крестовины. Меняя грузы, т.е. моменты сил, и момент инерции, можно убедиться, что угловое ускорение возрастает при увеличении момента силы или уменьшении момента инерции.
5.3. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Рассмотрим частный случай вращательного движения, когда суммарный момент внешних сил равен нулю. Как видно из (5.37), dL/dt = 0 при М = 0, откуда
Это положение известно под названием закона сохранения момента импульса: если суммарный момент всех внешних сил, действующих на тело, равен нулю, то момент импульса этою тела остается постоянным.
Опуская доказательство, отметим, что закон сохранения момента импульса справедлив не только для абсолютно твердого тела.
Наиболее интересные применения этого закона связаны с вращением системы тел вокруг общей оси. При этом необходимо учитывать векторный характер момента импульса и угловых скоростей. Так, для системы, состоящей из N тел, вращающихся вокруг общей оси, закон сохранения момента импульса можно записать в форме:
Рассмотрим некоторые примеры, иллюстрирующие этот закон.
Гимнаст, выполняющий сальто (рис. 5.11), в начальной фазе сгибает колени и прижимает их к груди, уменьшая тем самым момент инерции и увеличивая угловую скорость вращения вокруг горизонтальной оси, проходящей через центр масс. В конце прыжка тело выпрямляется, момент инерции возрастает, угловая скорость уменьшается. Фигурист, совершающий вращение вокруг вертикальной оси (рис. 5.12), в начале вращения приближает руки к корпусу, тем самым уменьшая момент инерции и увеличивая угловую скорость. В конце вращения происходит обратный процесс: при разведении рук увеличивается момент инерции и уменьшается угловая скорость, что позволяет легко остановиться.
Такое же явление может быть продемонстрировано на скамье Жуковского, которая представляет собой легкую горизонтальную платформу, вращающуюся с малым трением вокруг вертикальной оси. При изменении положения рук изменяются момент инерции и угловая скорость (рис. 5.13), момент импульса остается постоянным. Для усиления демонстрационного эффекта в руках человека гантели. На скамье Жуковского можно продемонстрировать векторный характер закона сохранения момента импульса.
Экспериментатор, стоящий на неподвижной скамье, получает от помощника велосипедное колесо, вращающееся вокруг вертикальной оси (рис. 5.14, слева). В этом случае момент импульса системы человек и платформа-колесо определяется только моментом импульса колеса:
здесь J ч - момент инерции человека и платформы; J K и ω κ - момент инерции и угловая скорость колеса. Так как момент внешних сил относительно вертикальной оси равен нулю, то L сохраняется (L = const).
Если экспериментатор повернет ось вращения колеса на 180° (рис. 5.14, справа), то момент импульса колеса будет направлен противоположно первоначальному и равен J K ω K . Так как вектор момента импульса колеса изменяется, а момент импульса системы сохраняется, то неизбежно должен измениться и момент импульса, человека и платформы, он уже не будет равен нулю 1 . Момент импульса системы в этом случае
1 Небольшим несовпадением оси колеса с осью вращения платформы можно пренебречь.
По формуле (5.42) можно приближенно оценить момент инерции тела человека вместе с платформой, для чего необходимо измерить ω κ , ω 4 и найти J k . Способ измерения угловых скоростей равномерного вращения известен читателю. Зная массу колеса и предполагая, что в основном масса распределена по ободу, по формуле (5.22) можно определить J k . Для уменьшения ошибки можно утяжелить обод велосипедного колеса, проложив по нему специальные шины. Человек должен располагаться симметрично оси вращения.
Более простой вариант рассмотренной демонстрации состоит в том, что человек, стоящий на скамье Жуковского, сам приводит во вращение колесо, которое он держит на вертикальной оси. При этом человек и платформа начинают вращаться в противоположные стороны (рис. 5.15).
5.4. ПОНЯТИЕ О СВОБОДНЫХ ОСЯХ ВРАЩЕНИЯ
Тело, вращающееся вокруг фиксированной оси, в общем случае действует на подшипники или другие устройства, которые сохраняют неизменным положение этой оси. При больших угловых скоростях и моментах инерции эти воздействия могут быть значительными. Однако в любом теле можно выбрать такие оси, направление которых при вращении будет сохраняться без каких-либо специальных устройств. Чтобы понять, какому условию должен удовлетворять выбор таких осей, рассмотрим следующий пример.
Сопоставляя (5.43) с координатами центра масс, замечаем, что силы, действующие на ось, уравновешиваются, если ось вращения проходит через центр масс.
Таким образом, если ось вращения проходит перпендикулярно стержню через центр масс, то воздействия на эту ось со стороны вращающегося тела не будет. Если при этом убрать подшипники, то ось вращения начнет перемещаться, сохраняя неизменным положение в пространстве, а тело будет продолжать вращение вокруг этой оси.
Оси вращения, которые без специального закрепления сохраняют свое направление в пространстве, называют свободными. Примерами таких осей являются оси вращения Земли и волчка, ось всякого брошенного и свободно вращающегося тела и т.п.
У тела произвольной формы всегда имеется по крайней мере три взаимно перпендикулярные оси, проходящие через центр масс, которые могут быть свободными осями вращения. Эти оси называют главными осями инерции. Хотя все три главные оси инерции являются свободными, наиболее устойчивым будет вращение вокруг оси с наибольшим моментом инерции. Дело в том, что в результате неизбежного действия внешних сил, например трения, а также в связи с тем, что трудно задать вращение точно вокруг определенной оси, вращение вокруг остальных свободных осей неустойчиво.
В некоторых случаях, когда тело вращается около свободной оси с малым моментом инерции, оно само изменяет эту ось на ось с наибольшим моментом.
Это явление демонстрируют следующим опытом. К электродвигателю подвешена на нити цилиндрическая палочка, которая может вращаться вокруг своей геометрической оси (рис. 5.17, а). Момент инерции относительно этой оси J 1 = тR 2 /2. При достаточно большой угловой скорости палочка изменит свое положение (рис. 5.17, б). Момент инерции относительно новой оси равен J 2 = ml 2 /12. Если l 2 >6R 2 , то и J 2 > J 1 . Вращение вокруг новой оси будет устойчивым.
Читатель может самостоятельно на опыте убедиться, что вращение брошенной спичечной коробки устойчиво относительно оси, проходящей перпендикулярно большей грани, и неустойчиво или менее устойчиво относительно осей, проходящих перпендикулярно другим граням (см. рис. 5.8).
Вращение животных и человека в свободном полете и при различных прыжках происходит вокруг свободных осей с наибольшим или наименьшим моментом инерции. Так как положение центра масс зависит от позы тела, то при разных позах будут и различные свободные оси.
5.5. ПОНЯТИЕ О СТЕПЕНЯХ СВОБОДЫ
Положение свободной материальной точки в пространстве задается тремя независимыми координатами: х, у, z. Если точка не свободна, а перемещается, например, по некоторой поверхности, то не все три координаты будут независимыми.
Независимые переменные, характеризующие положение механической системы, называют степенями свободы.
У свободной материальной точки три степени свободы, в рассмотренном примере - две степени свободы. Так как молекулу одноатомного газа можно рассматривать как материальную точку, следовательно, такая свободная молекула тоже имеет три степени свободы.
Еще некоторые примеры.
Две материальные точки 1 и 2 жестко связаны друг с другом. Положение обеих точек задано шестью координатами x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , на которые наложены одно ограничение и одна связь, математически выражаемая в форме уравнения:
Физически это означает, что расстояние между материальными точками всегда l. В этом случае число степеней свободы равно 5. Рассмотренный пример является моделью двухатомной молекулы.
Три материальные точки 1, 2 и 3 жестко связаны друг с. другом. Девять координат характеризуют положение такой системы: x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , x 3 , y 3 , z 3 . Однако три связи между точками обусловливают независимость только шести координат. Система имеет шесть степеней свободы. Так как положение трех точек, не лежащих на одной прямой, однозначно определяет положение твердого тела, то и твердое тело имеет шесть степеней свободы.
Такое же число степеней свободы (шесть) имеют трехатомные и многоатомные молекулы, если эти молекулы рассматривать как жесткие образования.
1 Если для зависимой координаты из (5.44) получают мнимую величину, это означает, что выбранные независимые координаты не соответствуют каким-либо точкам, расположенным на сфере заданного радиуса.
В реальных многоатомных молекулах атомы находятся в колебательных движениях, поэтому число степеней свободы таких молекул более шести.
Число степеней свободы определяет не только число независимых переменных, характеризующих положение механической системы, но и, что очень важно, число независимых перемещений системы. Так, три степени свободы свободной материальной точки означают, что любое перемещение точки можно разложить на независимые перемещения по трем осям координат. Так как точка не имеет размеров, то говорить о ее вращении не имеет смысла. Итак, материальная точка имеет три степени свободы поступательного движения. Материальная точка на плоскости, сфере или иной поверхности имеет две степени свободы поступательного движения. Перемещение материальной точки вдоль кривой (условный пример - движение поезда по рельсам) соответствует одной степени свободы поступательного движения.
Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы вращательного движения. Колесо поезда имеет две степени свободы: одна - вращательного движения, а другая - поступательного (перемещение оси колеса вдоль рельса). Шесть степеней свободы твердого тела означают, что любое перемещение этого тела можно разложить на составляющие: перемещение центра масс раскладывается на три поступательных движения по осям координат, а вращение состоит из трех более простых поворотов относительно осей координат, проходящих через центр масс.
На рис. 5.18-5.20 показаны шарнирные соединения, соответствующие одной, двум и трем степеням свободы.
Рис. 5.18
Рис. 5.19
Рис. 5.20
5.6. ЦЕНТРИФУГИРОВАНИЕ
Центрифугированием называется процесс разделения (сепарации) неоднородных систем, например частиц от жидкостей, в которых они находятся, обусловленный их вращением.
Рассмотрим разделение неоднородных систем в поле силы тяжести. Предположим, что имеется водная суспензия частиц различной плотности. Со временем благодаря действию силы тяжести и выталкивающей силы F A происходит расслаивание частиц: частицы с большей, чем у воды, плотностью тонут, частицы с меньшей, чем у воды, плотностью всплывают. Результирующая сила, действующая, например, на более плотную отдельную частицу, равна:
где ρ 1 - плотность вещества частицы; ρ - плотность воды; V - объем частицы.
Если значения ρ 1 и ρ мало отличаются друг от друга, то сила F p мала и расслоение (осаждение) происходит достаточно медленно. В центрифуге (сепараторе) такое разделение производят принудительно, вращая разделяемую среду.
Рассмотрим физику этого явления.
Пусть рабочий объем центрифуги (рис. 5.21: а - внешний вид; б - схема рабочего объема) полностью занят какой-либо однородной жидкостью. Выделим мысленно небольшой объем V этой жидкости, находящийся на расстоянии r от оси вращения OO". При равномерном вращении центрифуги на выделенный объем кроме силы тяжести и выталкивающей силы, которые уравновешивают друг друга, действует центростремительная сила. Это сила со стороны окружающей объем жидкости. Она, естественно, направлена к оси вращения и равна:
где ρ - плотность жидкости.
Предположим теперь, что выделенный объем V - это сепарируемая частица, плотность вещества которой ρ 1 (ρ 1 Φ ρ). Сила, действующая на частицу со стороны окружающей жидкости, не изменится, как это видно из формулы (5.45).
Для того чтобы частица вращалась вместе с жидкостью, на нее должна действовать центростремительная сила, равная:
где m 1 - масса частицы, а ρ 1 - соответствующая ей плотность.
Рис. 5.21
Если F > F 1 , то частица перемещается к оси вращения. Если F < F 1 , то воздействия на частицу со стороны жидкости будет недостаточно, чтобы удержать ее на круговой траектории, и частица по инерции начнет перемещаться к периферии. Эффект сепарации определяется превышением силы F, действующей со стороны жидкости на выделенную частицу, над тем значением центростремительной силы F 1 , которое обусловливает движение по окружности:
Это выражение показывает, что эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения 1 .
Сравним разделение центрифугированием с разделением с помощью силы тяжести:
1 Сила тяжести и выталкивающая сила при выводе формулы (5.47) не учитываются, так как они направлены вдоль оси вращения и не оказывают принципиального влияния на центрифугирование.
Ультрацентрифуги способны разделить частицы размером менее 100 нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях для разделения биополимеров, вирусов и субклеточных частиц.
Быстрота сепарации особенно важна в биологических и биофизических исследованиях, так как со временем может существенно измениться состояние изучаемых объектов.